2020 12 05

種類数とエジソン演算子　Kind Numbers with Edison Operator

　１＋１は，２である．しかし，当然の結果ではない．なぜなら，そうならない代数系も作れるからだ．「泥団子に泥団子を合わせても泥団子である」という，常識を超える発見に言及したのが，のちの発明王エジソン少年である．このアイデアを素直に代数にすれば，１＋１＝１である．この代数が，実は広く使われていい代物であることを述べてみたい．

　１＋１＝１である状況は，自然にも人工物にも多く存在する．林に林を足しても林である．平文に平文を足しても平文である．同じ種類の事物を足し合わせても，その種類を超え出ないとき，１＋１＝１となる．つまり，量を表す数は通常の代数系で計算できるけれども，定性的な数を演算するには，このエジソンの代数系が必要になる．この定性的な数を「種類数」とここでは呼んでおきたい．では，１＋１＝３以上になる場合もありうるだろうか．ありうるのである．しかもたくさんある．

　石灰石に塩酸を加えると何種類の物質ができるか．塩化カルシウムと二酸化炭素と水の３種類であるから，１＋１＝３である．また，この反応を途中で停止させるとすれば，未反応の石灰石と塩酸が残っているはずなので，１＋１＝５以上になる可能性がある．つまり，化学反応で物質の種類の数を問題にする場合，エジソン代数が役立ってしまう．一般に，量を問題にしない系では，エジソン代数が使える．

　エジソン代数で使う演算子は，交換法則も分配法則も満たさない．加える順序が異なると違う反応結果を得るためである．従って，＋に代わり「÷（スターラーを二指で持ち攪拌する様子を象った）」を使うことにし，これをエジソン演算子と呼ぶことにする．エジソン演算子は自然数同士の演算のみを扱う．その解はひとつに定まらず，ある範囲に収まることが多い．この範囲解を[A..B]と表す．2から5の間なら，[2..5]と表す．

　エジソン演算の範囲解は，いくつかの種類に分類できる．A と B で大きいほうを Max，小さいほうを Min，AとBの和を Sum とすると，下の表のようにまとめられる．

　もし，6÷4＝[7..9]となるなら，混合であるし，6÷4＝[3..8]となるなら，溶解である．混合⊆溶解 であり，分解⊆化合 であり，溶解⊆化合 である．

　エジソン演算の範囲解の中から，特定の値を推定する際に使う図が，融合分化図である．例として，5÷3＝[2..6] という式を考える．

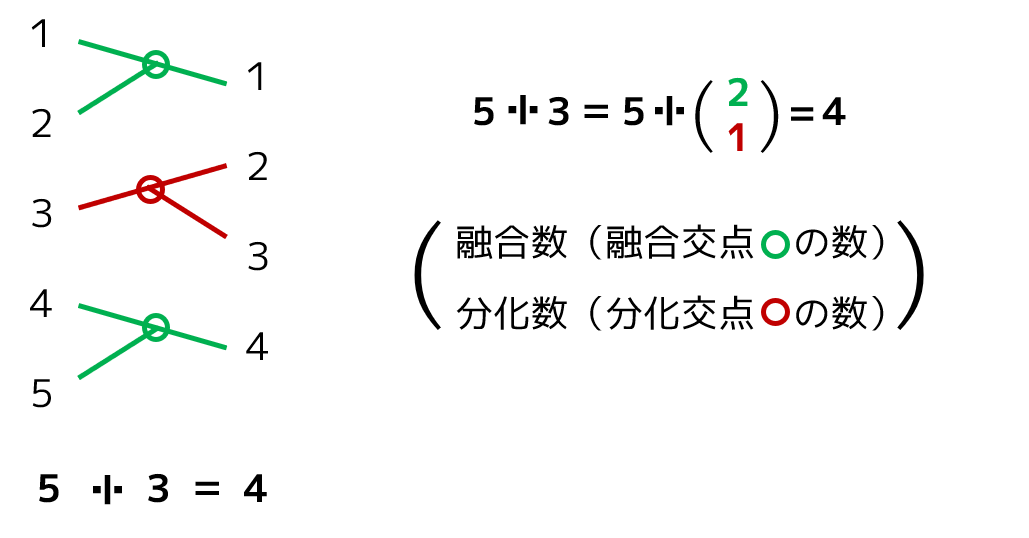
　上図左側が融合分化図である．5÷3という式の解は，[2..6]のどこかに収まる．もし解が 4 なら，5 と 4 を結び，かつ融合数と分化数の和が 3 であるような融合分化図が必ず書ける．上図右上では，融合数と分化数を ( ) に入れ，融合数を上に，分化数を下に記している．また，融合交点や分化交点は，3本以上の融合線または3本以上の分化線をひとつに束ねることを許す概念である．この融合分化図により，演算の結果が確定する．エジソン代数がどのような計算をする系なのか，少しだけでもお分かり頂けたら幸いである．

　この代数系は，単宇宙の誕生から死までや，多元宇宙の離合集散を，融合分化図で表せる．量が分からないほど大きすぎるものや，量を計算してもあまり意味のない長いものは，エジソン代数で来し方行く末を表せる．光に光を足しても光だけれど，光から万物が創られたのなら，厖大な回数の融合分化を果たしてきたはずである．そのうち私たちは光から創られたものたちに徐々に細かな固有名詞を付け，今では様々な単位で学名が付いている．そんな人間の分類活動をも表せるこのエジソン代数．神さまの初めから終わりまで計算することも，できない相談ではなさそうだ．