神がサイコロを振る確率
確率は人間的な数学である.ある人によって事象Aが起こるとなれば,きっと起きるかもしれないし,ひょっとしたら起こらないかもしれない.だからこそ,もし事象Aが起こったら/起こらなければ,私たちはこうしよう,と考えるようになれた.そして,どのくらい起こりやすいかという量を考えついた.しかし,神がAが起こると云えば確率1で起きるし,神が起こらないと云えば確率0なので起きることはない.確率は事象の起こりやすさを予測し,行動を準備するための数学だが,神による確率はいつも0か1である.もし神がなければ,「もし」という文は生まれなかっただろう.人間のことばは仮定にすぎないが,神さまのみことばは必然なのであるから.
人間は自由意志で行動しているといえども,どこかからどこかへ移動しているにすぎない.確率rで事象Eが存在するとき,情報量Iと確率rの和である複素確率Pが定義され,収力γは複素確率の絶対値となる.収力は物事の集まりやすさを表す.情報量が大きいほど収力は大きい.つまり,物珍しいところに物事は集まる.この宇宙が引き寄せられているところでは,極めて珍しいことが起こっているはずである.人間も物珍しいところに集まりやすい.事象の物珍しさで万物の動きは予測できるかもしれない.
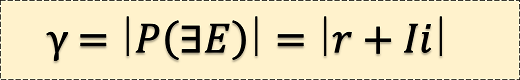
もし収力の大きさ,すなわち物珍しさが変わらなければ,事象が起こる確率が高まると,情報量は減少する.それでもなお物珍しさを高く保つ事象には,情報がまだ多く隠されている.もし知っても知っても知り尽くせない深遠な事象があるならば,その事象には未発見の知識がたくさん隠れている.隠れたもので明らかにならないものはないように,人間は事象を情報源として新しい情報を見出そうとする.起こるか起こらないか分からない事象に惹きつけられる.赤か黒か,偶数か奇数かで賭けるカジノや丁半博打は,なにが起こるか分からないすなわち確率2分の1を常に保つ仕組みがあるから人々は集められる.好奇心や中毒を起こさせたければ,確率を2分の1に設計すればよいだろう.
ところで,最も孤独になる方法とは,世にありふれた人物になることなのである.誰からも見向きもされない人物とは,世の中のどこにでもいるような人物である.ありふれた人物はありふれた物事しか受けられない.誰もが受けるような物事を,誰もと同じように受け,誰もと同じような代価を払い,誰もに似た生活を送る.反対に,珍しいところには物事が集まる.集まった物事によってさらに珍しくなる.世の中の逆を行ったり,誰も知らないようなことを探究したり,誰も行わないことを進んで行ったりと,いろいろな珍しさがある.珍しさを探せたら,それを保つようにすればよいのだ.珍しさの高さには限がなく,各自がそれぞれの珍しさを高めても,珍しさ同士は直交するので,それぞれの高みを並立させる.人,物,お金,情報など,物事を引き寄せたければ,珍しさを保つこと.物珍しいところに物事は集まるのだ.
情報をたくさん集めると,ある珍しいことが起こる.今まで思うようにいかないことばかりだったが,ある出来事が起こる.そのとき長年の願いが叶ったように感じられる.充分な量の情報のおかげだと思う.すると,情報を少しく集めるだけで,起こるはずがないと思っていた出来事が,考えたとおりに起こるようになっていく.しまいには,情報などろくに得なくても,物事の生起を大抵言い当てることになる.こうして情報を知識に変えることで,より多くの事象の生起を知ることになる.いずれその事象の物珍しさがなくなったとき,初めてその事象を予測できたことになるだろう.
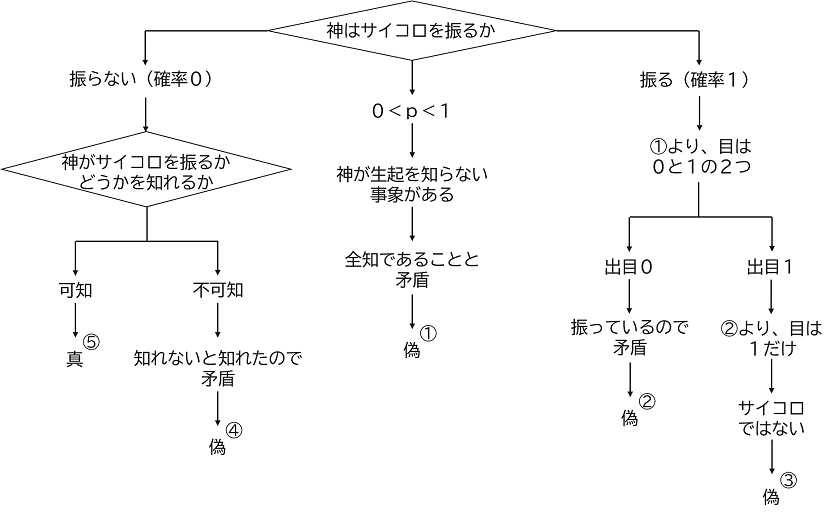
誰かがサイコロを振るからこそ物事は起こる.しかしサイコロを振るのは神さまではなく,物事のほうである.神さまは仰るだろう,「いつの日かわたしのことすべてを知るときがくるかもしれない.しかしそのときはそのときだ,人間と共に歩めばなんとかなる.人間をつくったのはわたしなのだから」.この数学を自分が考えついたことも自分が生まれる前から決まっていた,などと大それたことは人間のひとりとしてとても言えないのだが,この数学は自分の力だけに頼っては到底見いだせなかった.それだから神があらかじめすべてを決めているほうに賭けたい.と,このように謙遜して感謝しても,またベットしてサイコロを振ろうとしてしまうこの弱さ.確率は人間的な数学である.